peter(星期八)

CS기초 개념, NLP, 웹 관련 포스팅을 합니다. 매일 책을 읽고 달리기를 좋아하는 machine learning enthusiast 입니다. 반갑습니다. ^^

reading paper - Sample debiasing, Themis

13 minute read

TODO…

Open world database management system. THEMIS: Open world database.

TODO…

현재추세 분석 - 데이터 샘플에 액세스 및 분석 점검 용이해짐. python 같은 데이터 분석 toolkit 이 주류가 되고있음. 이로인해 데이터 과학이 샘플 분석과 밀접해짐. 근데 문제는 분석하려는 데이터 샘플이 항상 샘플링된 모집단을 정확히 나타내는것은 아니라는 점. 예를 들면 Twitter 샘플에서 Migration pattern 연구 시 샘플 선택 bias 현상있음. 데이터 소스에서 샘플링 메커니즘 알려져 있지 않아 bias 수정 어려움. 즉 Horvitz-Thompson estimator 같은 일반 테크닉을 못씀. 그러나 점점 더 많은 데이터 소스 과학자들이 debiasing 위해 population aggregates 활용하고있음. 이러한 aggregates 는 debiasing 용이하게 하나, 프로세스를 따분하게하고 에러 발생이 쉬워짐. aggregates 를 사용하는 debiasing 의 일반적, 자동화 테크닉 적용 시스템 없음. Themis는 debiasing 프로세스 자동화, 캡슐화 하는 open world database management system(DMBS). 단순히 샘플과 합계 삽입하고 쿼리를 구하면 마치 쿼리가 population 에서 issued 된것처럼 적절한 결과를 얻음. Themis 는 open world DMBS임. 왜냐하면 관계를 샘플로 취급, 샘플에 없는 튜플 여전히 존재할 수 있다고 가정하기 때문임. Themis 시스템의 두가지 핵심은,

  1. reweighting the sample
  2. learning the probability distribution of the population

전자는 heavy hitter query에 정확히 응답 가능. 후자는 샘플에 없을 수 있는 튜플에 대한 처리에 응답 가능.

sample reweighting 위해 두가지 approach investigate함.

  1. modifying linear regression
  2. applying an existing aggregate fitting procedure

learning the probability distribution 위해 bayesian network 활용, 대략적 분포 세우는데 사용.

논문의 참신함은 두개의 분리된 debiasing 테크닉을 세운점과 그 둘을 통합해서 쿼리 응답의 시스템 으로 구현했다는 점. Themis는 관계를 샘플로 취급, population-level aggregates 사용해 sample selection bias 자동으로 수정. 논문 성과 요약:

  1. 대략적인 population 쿼리 응답에 대해 샘플을 취하고 population aggregates 하고 자동으로 데이터를 debias 하는 첫번째 open world database system.
  2. debiasing technic 의 개발과 응용, 그리고 그것들을 통합하는 참신한 하이브리드 접근법
  3. 빠른 preprocessing time 을 위한 2가지 최적화 테크닉: population aggregate pruning, 모델 단순화.
  4. naive scaling 접근법과 비교, Themis 가 heavy hitter tuple 에 응답시 median error 의 70% 개선을 보여주는 3가지 데이터셋에서의 실험.

MOTIVATING EXAMPLE

예를 들어, 미국 내 항공편 중 비행시간 0.5h 이하에 대해 분석한다고 가정함. 이때 dataset 은 sample 이라하자. 분석을 준비하는 방법은 3가지:

  1. 아무것도 안하고 skew 무시. uniformly 하게 rebalance.
  2. 실제 700m 항공편 존재할때 본인은 70만개 샘플 보유, dataset에 weight attribute 추가, 각 tuple 에 가중치 10씩 부여함으로써 각각의 tuple이 실제 세계의 10개의 튜플임을 나타냄.
  3. 매년 어떤 주에서 떠나는 항공편 N개가 존재한다고 했을때, 본인은 n개의 샘플 보유. 이때 각각의 항공편에 N/m의 가중치 부여.

전처리 한 후에 form의 point queries issuing을 시작함.

SELECT SUM(weight) AS num_flights
FROM flights WHERE flight_time <= 30min
AND origin_state = '<state>';

THEMIS MODEL

Themis는 sample과 population aggregates data를 사용해서 대략적인 population queries에 응답하는 모델을 build함. 여기서 model은 reweighted sample과 probabilistic model 둘다 사용하여 쿼리에 응답하도록 encapsulate 하기때문에 사용되어짐. 두 테크닉 모두 집계aggregate를 만족시켜야할 “제약”으로 취급함. (population aggregates는 정확할 필요없음)

가정

대략 n size, m개 속성의 $A={A_1, …, Am}$를 갖는 모집단 P를 가정. P는 존재하지 않거나 공공에 release 되지 않았기에 unavailable함. 크기$N_i$의 각 속성 $A_i$의 active domain은 discrete, ordered라고 가정. 사이즈 $n_s$의 P로부터 draw한 샘플을 S라 하면 S는 독립이고 균일은 아님. 각 $tuple\in P$, S에 포함될 확률 $Pr_S(t)$, subscript S는 샘플링 확률(or 샘플링 메카니즘 or propensity score 라고도함)을 나타냄. 이 확률은 not known apriori(선험적). \(\Gamma=\{G_{\gamma_i,COUNT(*)}(P):i=1, B\}\) 다차원 변수의 집계 B, COUNT(*) 쿼리의 결과의 집합인 $\Gamma$이고, 위 식은 모집단에 대해 계산된 감마를 표시한것임. 그 중 $G_{\gamma_i,COUNT(*)}(P)$는 차원 $d_i$의 집계 쿼리임. 즉 $\gamma_i \in A$, 각 집계 쿼리$\Gamma_i$는 $M_i$속성 value-count pairs의 집합을 반환. 표시는 다음과 같다: \(\Gamma_i=\{(a_{i,k},c_{i,k}):k=1,...,M_i\}\) 그중 $a_{i,k}$는 집계 i 의 그룹 k 와 연관된 $d_i$ 속성값의 벡터. $c_{i,k}$는 group’s count. $\bigcup_{i=1,B} \gamma_i \subset A$ 는 집계가 모든 도메인 속성을 포함하지 않을 수 있다는 뜻임. 각 $\Gamma_i$ 에 대해 모든 카운트의 합은 대략 P의 크기임. $N_j$ 는 $A_j$ 속성의 서로다른 values의 갯수.

집계 i의 모든 count 와 group values 개별적으로 참조하려면 $\overline{\Gamma_i}^C$ 와 $\overline{\Gamma_i}^A$ 를 사용.

모집단에 대해 user query Q가 제공되고, Themis 사용 정확동 향상 연구를 위해, simple pointer, top-k queries에 집중하기로 한다. 또한 P가 없으므로, S와 $\Gamma$ 가 주어진 Q(P)를 estimate 해야함.

Sec.4

Themis 가 어떻게 $M(\Gamma,s)$를 빌드하는지 봄. Themis 의 구성:

  1. reweighted sample
  2. probabilistic model

reweighted sample

각 튜플 t $(t\in S)$ 에는 가중치 $w(t)$ 가 할당됨. w(t)는 P 중 t 의 출현횟수임. P 의 쿼리는 가중치 튜플에서 실행되도록 변환됨. 만약 샘플링 메카니즘 $Pr_S(t)$알때, 각 튜플은 $1/Pr_S(t)$로 reweight되고 Horvitz-Thompson 쓸수있음. challenge는 sample mechanism이 없다는 것이다. simple approach는 w(t)를 $ P / S $으로 셋팅하여 균일한 reweighting을 하는것인데, 샘플이 bias 되어 결과적으로 정확도가 떨어짐. bias 수정하기위해 샘플 S와 집계정보 $\Gamma$사용하여 w(t)를 학습하는 두가지 솔루션을 제시:
  1. adapt linear regression
  2. apply Iterative Proportional Fitting(IPF)

Linear regression reweighting

튜플의 가중치가 t의 속성의 선형조합이라 가정하자. 다시말해 $t^{0/1}$은 the one-hot encoded tuple t를 나타내고, $w(t)=\beta \cdot t^{0/1}$, 그중 $\beta$는 가중치의 벡터이다. m은 집계에 의해 적용된 속성의 갯수를 표현해서, 가중치 학습시 오직 이 속성들만 사용.

Iterative proportional fitting

w(t)를 푸는 다른 방법은 모든 w(t) 독립, 직접풀수있다 가정하는 것이다. 즉 w(t)는 그것의 속성의 함수가 아니라고 하자는 말이다. demography의 population synthesis 에서 영감을 받아 Iterative Proportional Fitting 라는 테크닉 적용해 w(t)해결하자. IPF는 주어진 모집단 집계와 일치하도록 샘플가중치를 보정하기위한 단순 반복 procedure 이며, 전통적으로 cencus report 집계를 위한 몇 모집단의 대표하는 마이크로샘플 reweight에 쓰인다. 각각의 individual aggregate에 대해, 샘플에서 만족되지 않으면 참여하는 튜플의 가중치는 선택된 집계를 만족시키도록 rescale된다. 절차는 집계가 충족될 때까지 집계에대해 계속 반복됨. 반복 알고리즘은 이전과 동일한 incidence matrix $G^{0,1}$을 빌딩하여 시작함. 그중 각 행은 single constraint 나타내고, 각 열은 S의 튜플 나타냄. y는 모든 집계 처리의 갯수값으로 구성된 벡터이다. 그러나 IPF 사용시엔 $X_S$가 없고 각 튜플의 가중치에 대한 $n_S$ 크기의 벡터 w를 가짐. 즉 $G^{0,1}w=y$ Alg 1 IPF에서 IPF의 수도코드 보여줌. 그중 [j]는 행렬일때 행j, 벡터일때 원소j 얻는것을 나타냄.

Linear regression과 Iterative proportional fitting을 통해 reweighted sample 테크닉을 실현하는 솔루션을 보았다. 두가지 다 w(t)을 푸는것이 목적이나, 선형 회귀에는 $m^{0,1}$파라메터가 있고 IPF에는 $n_S$ 파라메터 있음. 일반적으로 $m^{0,1} < n_S$ 또한 둘다 $\Sigma_{i=1,B}M_i$ 라는 제약을 가지므로 선형회귀는 over constrained, IPF는 under constrained임.

4.2 Probabilistic Model Learning

  1. 문제점: sample reweighting 언제 실패하는지 이해하는것 중요함.
    1. w(t)로 근사한 Horvitz-Thompson estimator가 샘플의 support가 모집단과 같다고 가정했을때임. 즉 $Pr_S(t)>0, \forall t$가 유지되지 않을때 sample reweighting 부정확해짐.
    2. support 동일하더라도, 튜플이 P내 존재, S내 부재일때, 샘플은 튜플이 존재하지 않는다 말하므로 그것이 실패함. rare group과 작은 샘플 사이즈에서 발생. S에다 누락된 행을 impute 할수있지만,
      1. 중요한 구조적 정보를 잃거나
      2. 쿼리 속도 저하 의 리스크가 있다.
  2. 솔루션: S, $\Gamma$ 사용하여 확률 모델 P를 빌드하고 이 모델을 가지고 쿼리에 응답. 확률 모델을 빌드할 때 고려할 점은 어던 분포 유형을 사용할 것이냐임. 모집단에 대해 우리는 사전 지식 없으므로, 집계 데이터로부터 학습할 수 있는 분포를 고려하기로 한다. BN(Baysian Network) 사용하여 모집단 분포를 모델링함. BN은 집계 쿼리로 매개변수화되고 많은 속성, 큰 데이터로 확장가능. 샘플만으로부터 BN 구축하는게 아니라 S, $\Gamma$ 를 BN학습에 병합함.

네트워크 구조 학습

greedy hill-climbing 알고리즘 적용함. 전통적 hill-climbing 알고리즘의 목표는 몇몇 스코어를 최대화하는 구조를 찾는것임. 알고리즘 각 단계에서 점수를 가장 많이 향상시키는 “move”한다. 그리고 더 개선할 게 없으면 종료. 이번에 수정한 알고리즘: 첫번째 단계서 $\Gamma$의 모든 속성이 네트워크에 추가될 때 까지 $\Gamma$를 사용하여 “move”한다. 그 다음, S에 있고 $\Gamma$에 없는 속성이 있으면 S를 사용하여 계속 빌드함.

네트워크 파라메터 학습

BN 파라메터는 BN 구조에 적용되는 데이터의 likelihood 를 최대화하여 학습됨. BN 파라메터 학습 최적화에 파라메터 쉐어링 제한을 추가하는 대신에 각 집계가 충족되게 하는 제한을 추가함. 집계에 참여하지 않는 속성들의 모든 가능한 값에 대한 조인트 확률을 합산하여, 참여하는 값들의 확룰을 계산함.

Hybrid query evaluator

OWQP 수행하기위해 Themis는 상술한 두가지 method를 통합한다. 포인트 쿼리가 발행 되었을때, 처리된 튜플이 샘플에 존재할때, reweighting sample 사용, 그렇지 않으면 BN 직접 추론. 쿼리 evaluator 에서 샘플에 없는 튜플만 BN answer 사용하여 캡쳐한다. 이 테크닉은 샘플을 취급할때 모집단과 동일한 support 가지지 않을때 효과적임.

Evaluation

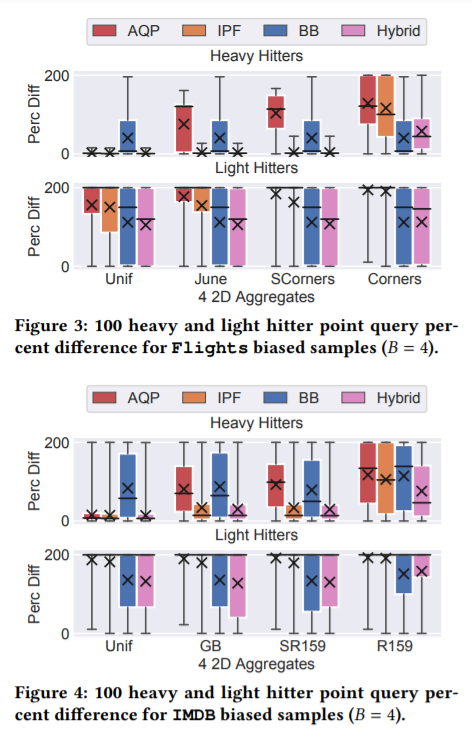
Themis의 OWQP 에 대한 정확성과 실행시간을 평가함. dataset은 항공 데이터셋과 IMDB 데이터셋을 사용함. 사전처리를 통해 null 값을 제거, 실제값 속성을 등가 버킷으로 bucketize 함. Flights 로부터 3가지 샘플을 취함: 균일(Unif), 6월의 항공편(June), CA, NY, FL, WA로부터의 항공편(SCorner). 각각은 90%의 bias를 가진 10%의 샘플임. 즉 90%의 행들은 selection criteria 로부터 가져온것임. fig34

  1. 전반적 정확도: Fig3,4보면, B=4, d=2일때의 Themis Hybrid(Pink), 표준 AQP(균일 reweighting, red), IPF의 best 선형 reweighting 테크닉(주황), BB의 베스트 BN 테크닉(파랑, BB는 BN 학습시 S, $\Gamma$사용의 의미). median value는 검정색 실선, everage는 검정색 X로 표시. Themis 하이브리드는 나머지 세개에 비해 가장 낮은 에러를 달성함. support가 같을수록 sample reweighting 기술은 훨씬 더 나아짐. Themis 하이브리드는 이러한 차이를 완화하고 100% bias 의 IPF 보다 나은 성능을 보여줌. 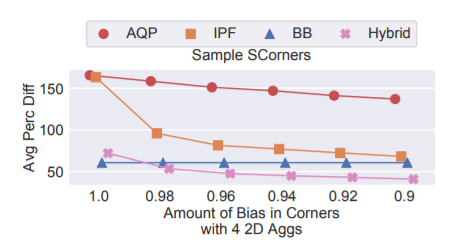fig5 Fig5는 더 복잡한 SQL쿼리에서 정확성에 대한 bias의 영향을 추가로 조사. 원과 수평선은 각각 “Corner”와 “SCorner”에서의 결과를 나타냄.
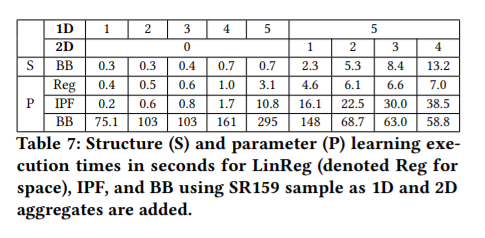  2. 실행시간: table7 IMDB의 SR159 샘플. reweighted sample 에 대해 쿼리 실행하는데 평균 25.3ms 소요. BN에서 직접 발행된 쿼리에는 평균 2.07ms 소요. 표7 보면 LinReg 가장 빠르고 그다음 IPF, BB순.

You may also enjoy

VS Code 에서 c/c++ 사용하기

2 minute read

windows에서 C/C++ IDE를 설치하지 않았을 때 컴파일러를 직접 다운받아 설치해야 하는데 이 때 여러 선택지가 있다. 그 중에서 TDM-GCC를 설명한다. TDM-GCC는 Windows친화적인 컴파일러라고 홈페이지에 설명되어 있다. 홈페이지에서 다운로드 가능하다.

Interview

4 minute read

바이트댄스 Interview에서 물어본 것들 생각 나는 것 위주로 정리하고 그 밖에 많이 올라온 문제들 소개하기로 한다. 크게 컴퓨터 네트워크, 자료구조, 컴퓨터 시스템(OS) 지식을 물었고 코딩은 두 문제 나왔다. 온라인이어서 어떻게 하는지 궁금했는데 중국의 nowcoder라는 ...